Hanya Manusia Biasa Part II: Trigonometri

Minggu, 10 November 2013

Trigonometri

trigonometri

Hubungan fungsi trigonometri

Fungsi dasar:

$\sin A = \frac{a}{c}\,$

$\cos A = \frac{b}{c}\,$

$\tan A = \frac{\sin A}{\cos A}\ = \frac{a}{b}\,$

$\cot A = \frac{1}{\tan A} = \frac{\cos A}{\sin A}\ = \frac{b}{a}\,$

$\sec A = \frac{1}{\cos A}\ = \frac{c}{b}\,$

$\csc A = \frac{1}{\sin A}\ = \frac{c}{a}\,$

$\sin {(-A)} = -\sin A$

$\cos {(-A)} = \cos A$

$\tan {(-A)} = - \tan A$

$\csc {(-A)} = - \csc A$

$\sec {(-A)} = \sec A$

$\cot {(-A)} = - \cot A$

Identitas trigonometri

$\sin^2 A + \cos^2 A = 1 \,$

$1 + \tan^2 A = \frac{1}{\cos^2 A} = \sec^2 A\,$

$1 + \cot^2 A = \frac{1}{\sin^2 A} = \csc^2 A \,$

Penjumlahan

$\sin (A + B) = \sin A \cos B + \cos A \sin B \,$

$\sin (A - B) = \sin A \cos B - \cos A \sin B \,$

$\cos (A + B) = \cos A \cos B - \sin A \sin B \,$

$\cos (A - B) = \cos A \cos B + \sin A \sin B \,$

$\tan (A + B) = \frac{\tan A + \tan B}{1 - \tan A \tan B} \,$

$\tan (A - B) = \frac{\tan A - \tan B}{1 + \tan A \tan B} \,$

$sin(u)+sin(v)=2sin(\frac {u+v}{2})cos(\frac{u-v}{2})$

$sin(u)-sin(v)=2cos(\frac {u+v}{2})sin(\frac{u-v}{2})$

$cos(u)+cos(v)=2cos(\frac {u+v}{2})cos(\frac{u-v}{2})$

$cos(u)-cos(v)=-2sin(\frac{u+v}{2})sin(\frac{u-v}{2})$

Perkalian

$2 \sin A \times \cos B = \sin (A + B) + \sin (A - B),$

$2 \cos A \times \sin B = \sin (A + B) - \sin (A - B),$

$2 \cos A \times \cos B = \cos (A + B) + \cos (A - B),$

$2 \sin A \times \sin B = - \cos (A + B) + \cos (A - B),$

Rumus sudut rangkap dua

$\sin 2A = 2 \sin A \cos A \,$

$\cos 2A = \cos^2 A - \sin^2 A = 2 \cos^2 A -1 = 1-2 \sin^2 A \,$

$\tan 2A = {2 \tan A \over 1 - \tan^2 A} = {2 \cot A \over \cot^2 A - 1} = {2 \over \cot A - \tan A} \,$

Rumus sudut rangkap tiga

$\sin 3A = 3 \sin A - 4 \sin^3 A \,$

$\cos 3A = 4 \cos^3 A - 3 \cos A \,$

Rumus setengah sudut

$\sin \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{2}} \,$

$\cos \frac{A}{2} = \pm \sqrt{\frac{1+\cos A}{2}} \,$

$\tan \frac{A}{2} = \pm \sqrt{\frac{1-\cos A}{1+\cos A}} = \frac {\sin A}{1+\cos A} = \frac {1-\cos A}{\sin A} \,$

Aturan Sinus, Cosinus, dan Tangen

Aturan sinus

$\frac{a}{\sin A} \,=\, \frac{b}{\sin B} \,=\, \frac{c}{\sin C} \!$

Turunan dari aturan sinus

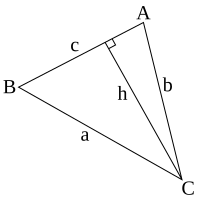
Law of sines proof.svg

Luasan dari segitiga diatas dapat dirumuskan sebagai

$L = \frac{1}{2}bc \sin A = \frac{1}{2}ac \sin B = \frac{1}{2}ab \sin C\,.$

Kalikan persamaan diatas dengan $2/abc$ maka akan menjadi

$\frac{2L}{abc} = \frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}\,.$

Aturan cosinus

Triangle with notations 2.svg

$c^2 = a^2 + b^2 - 2ab\cos\gamma\ ,$

$a^2 = b^2 + c^2 - 2bc\cos\alpha\,$

$b^2 = a^2 + c^2 - 2ac\cos\beta\,$

Aturan tangen

Triangle with notations 2.svg

http://id.wikibooks.org/wiki/Subjek:Matematika/Materi:Trigonometri $\frac{a-b}{a+b} = \frac{\tan[\frac{1}{2}(\alpha-\beta)]}{\tan[\frac{1}{2}(\alpha+\beta)]}.$

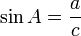
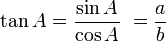
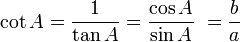
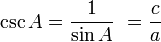
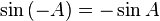
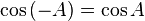
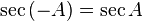
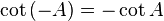
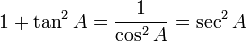
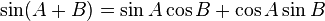
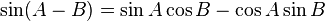
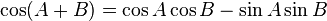
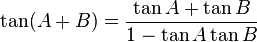
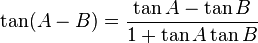
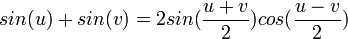
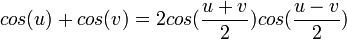
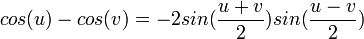
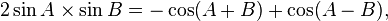
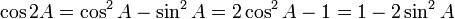
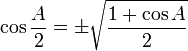
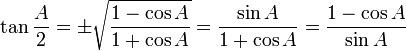
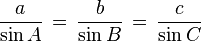
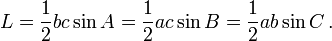
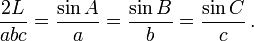
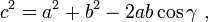
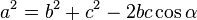
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)